Componenti analogiche di bassa frequenza

L'inviluppo complesso $\underline{x}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$e^{j$\varphi$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$} può ovviamente essere espresso tramite le sue parti reale ed immaginaria: $\underline{x}$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$cos$\varphi$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ + ja$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$sin$\varphi$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ + jx_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$. I segnali x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$cos$\varphi$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ed x_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$sin$\varphi$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ prendono il nome di componenti analogiche di bassa frequenza di x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ per un motivo presto chiaro. Intanto sviluppiamo^8.10 l'espressione del corrispondente segnale modulato:

x$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$	=	$$\Re$$$$\left\{\vphantom{ \underline{x}\left( t\right) e^{j\omega _{0}t}}\right.$$$$\underline{x}$$$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ej$\omega_{0}$t$$\left.\vphantom{ \underline{x}\left( t\right) e^{j\omega _{0}t}}\right\}$$ = a$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$cos$$\left(\vphantom{ \omega _{0}t+\varphi \left( t\right) }\right.$$$$\omega_{0}^{}$$t + $$\varphi$$$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ $$\left.\vphantom{ \omega _{0}t+\varphi \left( t\right) }\right)$$ = a$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$$$\left[\vphantom{ \cos \omega _{0}t\cos \varphi \left( t\right) -\sin \omega _{0}t\sin \varphi \left( t\right) }\right.$$cos$$\omega_{0}^{}$$tcos$$\varphi$$$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ - sin$$\omega_{0}^{}$$tsin$$\varphi$$$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$ $$\left.\vphantom{ \cos \omega _{0}t\cos \varphi \left( t\right) -\sin \omega _{0}t\sin \varphi \left( t\right) }\right]$$
	=	xc$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$cos 2$$\pi$$f0t - xs$$\left(\vphantom{ t}\right.$$t$$\left.\vphantom{ t}\right)$$sin 2$$\pi$$f0t

0.350000

 

Il risultato ottenuto è valido per un qualunque segnale; ma riveste una importanza particolare nel caso in cui x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$) sia di tipo limitato in banda con banda 2W centrata attorno ad f₀, con W < f₀: in tal caso, sia x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ che x_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ risultano limitate in banda tra $\pm$W e contigue all'origine.

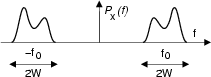
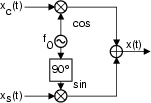
Che sia vero anche il viceversa, può essere verificato in modo intuitivo, partendo da x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ e x_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ limitate in banda, e moltiplicandole per coseno e seno. Quest'ultima osservazione ci mostra una via per sintetizzare un segnale modulato in ampiezza, od angolarmente, od entrambe le cose, mediante il semplice schema circuitale disegnato a fianco, che si basa sulla conoscenza delle componenti analogiche di bassa frequenza, che a loro volta sono ottenibili a partire da a$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ e $\varphi$$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$. Restano comunque (per ora) aperti i seguenti problemi:

• Noto x$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, come ottenere x_c$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ed x_s$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ ?
• Noto lo spettro di densità di potenza $\mathcal {P}$_x$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$, che dire di $\mathcal {P}$_{$\underline{x}$}$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ ?

Per procedere oltre occorre introdurre: