Periodogramma

Definiamo un intervallo T in cui isoliamo un segnale x_T$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ = x$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$rect_T$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$ da una realizzazione x_T$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$. Questo segmento di segnale è di energia, con $\mathcal {E}$_xT$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\left\vert\vphantom{ X_{T}\left( f\right) }\right.$X_T$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ $\left.\vphantom{ X_{T}\left( f\right) }\right\vert^{2}_{}$, e al quale si può attribuire una densità di potenza

$$\mathcal {P}$$_xT$$\left(\vphantom{ f}\right.$$f$$\left.\vphantom{ f}\right)$$ = $${\frac{\left\vert X_{T}\left( f\right) \right\vert ^{2}}{T}}$$

che viene detta periodogramma^7.11. Al tendere di T ad $\infty$, il risultato trovato tende alla densità di potenza $\mathcal {P}$_x$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\lim_{T\rightarrow \infty }^{}$${\frac{\left\vert X_{T}\left( f,\theta \right) \right\vert ^{2}}{T}}$ della realizzazione x_T$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$ e, se questa appartiene ad un processo ergodico, a quella di un qualunque altro membro.

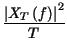
Nel caso più verosimile in cui T non tende ad infinito, tentiamo di valutare l'errore che si commette ad usare $\mathcal {P}$_xT$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ come una stima $\widehat{\mathcal{P}}_{x}^{}$$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ della vera densità $\mathcal {P}$_x$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ del processo. Per una determinata frequenza f₀, il valore ${\frac{\left\vert X_{T}\left( f_{0}\right) \right\vert ^{2}}{T}}$ è una variabile aleatoria (dipende infatti da $\theta$), che vorremmo avesse un valore atteso m_T = E_$\theta$$\left\{\vphantom{ \mathcal{P}_{x_{T}}\left( f_{0}\right) }\right.$$\mathcal {P}$_xT$\left(\vphantom{ f_{0}}\right.$f₀$\left.\vphantom{ f_{0}}\right)$ $\left.\vphantom{ \mathcal{P}_{x_{T}}\left( f_{0}\right) }\right\}$ pari alla densità del processo ( m_T = $\mathcal {P}$_x$\left(\vphantom{ f_{0}}\right.$f₀$\left.\vphantom{ f_{0}}\right)$) ed una varianza $\sigma_{T}^{2}$ = E_$\theta$$\left\{\vphantom{ \left( \mathcal{P}_{x_{T}}\left( f_{0}\right) -m_{T}\right) ^{2}}\right.$$\left(\vphantom{ \mathcal{P}_{x_{T}}\left( f_{0}\right) -m_{T}}\right.$$\mathcal {P}$_xT$\left(\vphantom{ f_{0}}\right.$f₀$\left.\vphantom{ f_{0}}\right)$ - m_T$\left.\vphantom{ \mathcal{P}_{x_{T}}\left( f_{0}\right) -m_{T}}\right)^{2}_{}$ $\left.\vphantom{ \left( \mathcal{P}_{x_{T}}\left( f_{0}\right) -m_{T}\right) ^{2}}\right\}$ che diminuisce la crescere di T^7.12. Per verificare se tali proprietà siano soddisfatte, valutiamo il valore atteso del periodogramma, a partire dal risultato $\left\vert\vphantom{ X_{T}\left( f_{0}\right) }\right.$X_T$\left(\vphantom{ f_{0}}\right.$f₀$\left.\vphantom{ f_{0}}\right)$ $\left.\vphantom{ X_{T}\left( f_{0}\right) }\right\vert^{2}_{}$ = $\mathcal {E}$_xT$\left(\vphantom{ f}\right.$f$\left.\vphantom{ f}\right)$ = $\mathcal {F}$$\left\{\vphantom{ \mathcal{R}_{x_{T}}\left( \tau \right) }\right.$$\mathcal {R}$_xT$\left(\vphantom{ \tau }\right.$$\tau$ $\left.\vphantom{ \tau }\right)$ $\left.\vphantom{ \mathcal{R}_{x_{T}}\left( \tau \right) }\right\}$:

$$\theta \left\{\vphantom{ \mathcal{P}_{x_{T}}\left( f_{0}\right) }\right. \mathcal {P} \left(\vphantom{ f_{0}}\right. \left.\vphantom{ f_{0}}\right) \left.\vphantom{ \mathcal{P}_{x_{T}}\left( f_{0}\right) }\right\} \theta \left\{\vphantom{ \mathcal{F}\left\{ \frac{1}{T}\int _{-\infty }^... ...right) x\left( t+\tau \right) rect_{T}\left( t+\tau \right) dt\right\} }\right. \mathcal {F} \left\{\vphantom{ \frac{1}{T}\int _{-\infty }^{\infty }x\left( t\... ...\left( t\right) x\left( t+\tau \right) rect_{T}\left( t+\tau \right) dt}\right. {\frac{1}{T}} \int_{-\infty }^{\infty } \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \left(\vphantom{ t+\tau }\right. \tau \left.\vphantom{ t+\tau }\right) \left(\vphantom{ t+\tau }\right. \tau \left.\vphantom{ t+\tau }\right) \left.\vphantom{ \frac{1}{T}\int _{-\infty }^{\infty }x\left( t\r... ...left( t\right) x\left( t+\tau \right) rect_{T}\left( t+\tau \right) dt}\right\} \left.\vphantom{ \mathcal{F}\left\{ \frac{1}{T}\int _{-\infty }^{... ...ight) x\left( t+\tau \right) rect_{T}\left( t+\tau \right) dt\right\} }\right\}$$ =

$$\mathcal {F} \left\{\vphantom{ \frac{1}{T}\int _{-\infty }^{\infty }E_{\theta ... ...ight) \right\} rect_{T}\left( t\right) rect_{T}\left( t+\tau \right) dt}\right. {\frac{1}{T}} \int_{-\infty }^{\infty } \theta \left\{\vphantom{ x\left( t\right) x\left( t+\tau \right) }\right. \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \left(\vphantom{ t+\tau }\right. \tau \left.\vphantom{ t+\tau }\right) \left.\vphantom{ x\left( t\right) x\left( t+\tau \right) }\right\} \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \left(\vphantom{ t+\tau }\right. \tau \left.\vphantom{ t+\tau }\right) \left.\vphantom{ \frac{1}{T}\int _{-\infty }^{\infty }E_{\theta }... ...ght) \right\} rect_{T}\left( t\right) rect_{T}\left( t+\tau \right) dt}\right\}$$ =

$$\mathcal {F} \left\{\vphantom{ \mathcal{R}_{x}\left( \tau \right) \frac{1}{T}\... ...fty }^{\infty }rect_{T}\left( t\right) rect_{T}\left( t+\tau \right) dt}\right. \mathcal {R} \left(\vphantom{ \tau }\right. \tau \left.\vphantom{ \tau }\right) {\frac{1}{T}} \int_{-\infty }^{\infty } \left(\vphantom{ t}\right. \left.\vphantom{ t}\right) \left(\vphantom{ t+\tau }\right. \tau \left.\vphantom{ t+\tau }\right) \left.\vphantom{ \mathcal{R}_{x}\left( \tau \right) \frac{1}{T}\i... ...ty }^{\infty }rect_{T}\left( t\right) rect_{T}\left( t+\tau \right) dt}\right\} \mathcal {F} \left\{\vphantom{ \mathcal{R}_{x}\left( \tau \right) \cdot \hbox {tri}_{2T}\left( \tau \right) }\right. \mathcal {R} \left(\vphantom{ \tau }\right. \tau \left.\vphantom{ \tau }\right) \left(\vphantom{ \tau }\right. \tau \left.\vphantom{ \tau }\right) \left.\vphantom{ \mathcal{R}_{x}\left( \tau \right) \cdot \hbox {tri}_{2T}\left( \tau \right) }\right\}$$ =

$$\mathcal {P} \left(\vphantom{ f}\right. \left.\vphantom{ f}\right) \left(\vphantom{ \hbox {sinc}\left( fT\right) }\right. \left(\vphantom{ fT}\right. \left.\vphantom{ fT}\right) \left.\vphantom{ \hbox {sinc}\left( fT\right) }\right)^{2}_{}$$ =

che ci ripropone il risultato ottenuto al §3.9 relativo al processo di finestratura, e che mostra come lo stimatore è polarizzato^7.13. In base allo scopo con cui è condotta la stima spettrale, può essere opportuno adottare al posto della finestra rettangolare un diverso andamento w_T$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$, in modo da calcolare x_T$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$ = x$\left(\vphantom{ t,\theta }\right.$t,$\theta$ $\left.\vphantom{ t,\theta }\right)$w_T$\left(\vphantom{ t}\right.$t$\left.\vphantom{ t}\right)$.

Il calcolo del periodogramma viene svolto mediante una Trasformata Discreta di Fourier (DCT), o meglio ancora con una FFT. In tal caso, l'aumento di T corrisponde all'aumento del numero di campioni utilizzati, e all'aumento della risoluzione in frequenza ottenibile. In base a queste considerazioni, si può mostrare che la varianza dello stimatore non decresce con T.